Ellipse

An ellipse is a geometric shape that looks like a stretched circle or a flattened oval. It is defined by two points called the foci and a constant sum of distances from these foci to any point on the ellipse. This sum is constant for every point on the ellipse, which gives it its unique shape.

Ellipses can be found in various natural and man-made objects, from planetary orbits to the design of wheels and arches. They have several unique properties, such as symmetry along their major and minor axes, which makes them useful in many areas of mathematics and physics.

In this article, we will discuss the ellipse in detail including its properties, equations, and real-world examples.

What is Ellipse?

An ellipse is a two-dimensional closed-plane curve which looks like an oval or a flattened circle. When a cone is intersected by a plane at an angle with respect to its base, an ellipse is created. If the plane intersected by the cone is parallel to the base, then it forms a circle.

Ellipse Definition

An ellipse is defined as a collection of all points in a plane such that the sum of the distances from two fixed points (called the foci) is constant.

Let F₁​ and F₂​ be the foci of the ellipse, and let 2a be the length of the major axis. Then, the ellipse can be defined by the equation:

∣PF₁​∣ + ∣PF₂​∣= 2a

Where,

• P is any point on the ellipse.
• ∣PF₁​∣ denotes the distance from P to the first focus F₁​.
• ∣PF₂​∣ denotes the distance from P to the second focus F₂​.

Shape of Ellipse

In geometry, an ellipse is a two-dimensional shape that is defined by its axes. An ellipse looks like an elongated circle or similar to an oval. If you have observed the shapes of eggs, badminton rackets, or balloons, you’ll notice they are somewhat similar to the shape of an ellipse.

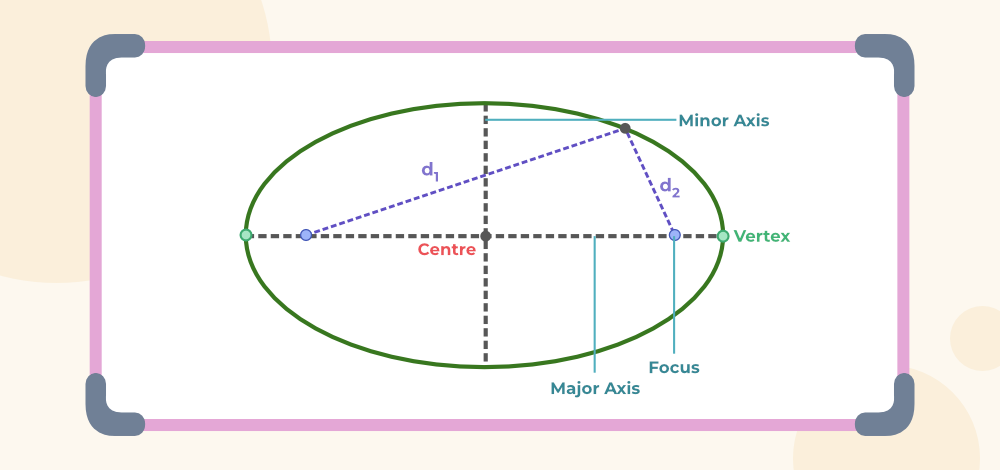
Parts of Ellipse

Most common parts of any ellipse are:

• Center: The midpoint of the major axis of an ellipse; the point equidistant from the foci and defining the geometric symmetry of the ellipse.

• Foci: In an ellipse, the foci (singular: focus) are two fixed points used to define the shape of the ellipse. The sum of the distances from any point on the ellipse to the two foci is constant.

• Vertex: Points on the ellipse where the major and minor axes intersect the ellipse. In an ellipse, there are typically four vertices.

• Directrix: For any point on an ellipse, the ratio of its distance to the focus and its distance to the directrix is a constant, known as the eccentricity of the ellipse.

• Major Axis: The major axis of an ellipse is the longest diameter, passing through the two foci, and it is also the longest segment that can be drawn across the ellipse.

• Minor Axis: The minor axis of an ellipse is the shortest diameter, perpendicular to the major axis, and passing through the center of the ellipse.

• Latus Rectum: The latus rectum of an ellipse is a line segment that passes through one of the foci and is parallel to the minor axis.

• Conjugate Axis: Conjugate axis of an ellipse is another name for the minor axis. It is perpendicular to the transverse axis (major axis) and passes through the center of the ellipse.

• Transverse Axis: Transverse axis of an ellipse is another name for the major axis. It is the longest diameter of the ellipse and passes through the center.

Equation of Ellipse

There are many forms of equation of ellipse, some of these are:

• Standard Form
• General Form
• Parametric Equation

Standard Form of Ellipse Equation

The ellipse equation with its center at the origin and its major axis along the x-axis is:

x²/a²+y²/b² = 1

Where,

• a is the length of the semi-major axis (half the distance of the major axis).
• b is the length of the semi-minor axis (half the distance of the minor axis).
• The major axis is along the horizontal direction if a>b.

The ellipse equation with the center at the origin and the major axis along the y-axis is:

x²/b²+y²/a² = 1

Where,

• a is the length of the semi-major axis (half the distance of the major axis).
• b is the length of the semi-minor axis (half the distance of the minor axis).
• The major axis is along the vertical direction if a>b.

General Form of Ellipse Equation

The general form of the equation of an ellipse in Cartesian coordinates is:

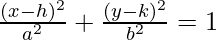
Where,

• (h, k) represents the coordinates of the center of the ellipse.
• a and b are the lengths of the semi-major axis and semi-minor axis respectively.

Note: When a = b, the ellipse becomes a circle.

Parametric Equation of Ellipse

The parametric equations of an ellipse in Cartesian coordinates can be written as follows:

x(t) = h + a cos (t) and y(t) = k + b sin (t)

Where,

• (h, k) represents the coordinates of the center of the ellipse,
• a and b are the lengths of the semi-major axis and semi-minor axis respectively,
• t is the parameter that ranges from 0 to 2π (or any multiple of 2π for multiple loops), and
• (x(t), y(t)) gives the coordinates of points on the ellipse as t varies.

Ellipse Formula

For equation x²/b²+y²/a² = 1, if c is the distance between both focii is c, then formula for ellipse is given as:

c²= a² – b²

Derivation of Equation of Ellipse

The figure represents an ellipse such that P₁F₁ + P₁F₂ = P₂F₁ + P₂F₂ = P₃F₁ + P₃F₂ is a constant. This constant is always greater than the distance between the two foci. When both the foci are joined with the help of a line segment then the mid-point of this line segment joining the foci is known as the centre.

The image given below shows the foci F₁ and F₂ of the ellipse and points P₁, P_2, and P₃ are points on the circumference of the ellipse.

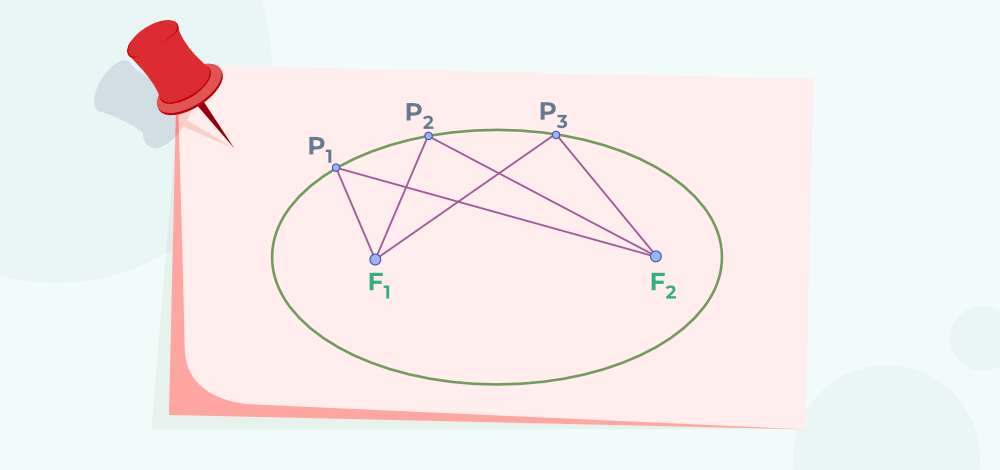
The line segment passing through the foci of the ellipse is the major axis and the line segment perpendicular to the major axis and passing through the centre of the ellipse is the minor axis. The endpoints P and Q as shown are known as the vertices which represent the intersection of major axes with the ellipse. ‘2a’ denotes the length of the major axis and ‘a’ is the length of the semi-major axis. ‘2b’ is the length of the minor axis and ‘b’ is the length of the semi-minor axis. ‘2c’ represents the distance between two foci.

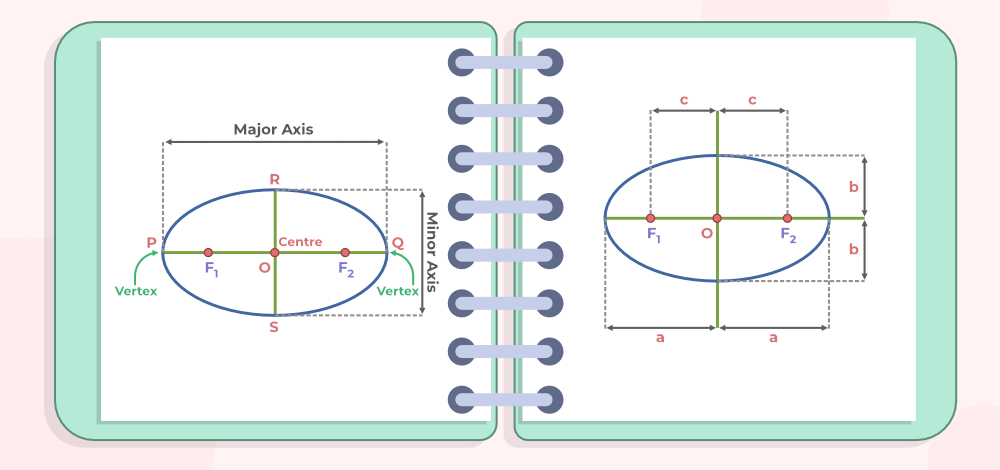
Proof:

Let’s take P and Q as the endpoint of the major axis and points R and S at the end of the minor axis and O as the centre of the ellipse.

Distances of Q from F₁ is F₁Q and Q to F₂ is F₂Q and their sum is F₁Q + F₂Q and F₁Q + F₂Q = F₁O + OQ + F₂Q

c + a + a – c = 2a

Sum of distances from point R to F₁ is F₁R + F₂R

F₁R + F₂R = √(b² + c²) + √(b² + c²)  = 2√(b² + c²)

By definition of the Ellipse,

2√(b² + c²) = 2a

⇒ a = √(b² + c²)

⇒ a² = b² + c²

⇒ c² = a² – b²

Properties of Ellipse

Various properties of an ellipse are,

• Ellipse includes two focal points, also referred to as foci.
• A fixed distance is referred to as a directrix.
• The eccentricity of an ellipse ranges from 0 to 1. 0 ≤ e < 1
• The whole sum of each distance from an ellipse’s locus to its two focal points is constant.
• Ellipse has one major and one minor axis, as well as a centre.

Eccentricity of Ellipse

The eccentricity of an ellipse is defined as the ratio of distances from the centre of the ellipse to the semi-major axis of the ellipse.

e = c/a

Where,

• c is the focal length, and
• a is the semi-major axis length.

The eccentricity of an ellipse is always larger than 1.

Furthermore, c² = a² – b^2.

As a result, eccentricity becomes:

e = √[(a² – b²)/a²]

⇒ e = √[1 – (b²/a²)]

Auxiliary Circle

Auxiliary circle of an ellipse is a circle constructed using center of ellipse as center and semi major axis as radius. It is positioned so that it touches the ellipse at its endpoints of the major axis (the vertices of the ellipse). For any ellipse with a as its semi major axis, (h, k) as its center, equation of auxiliary circle is given by:

(x – h)² + (y – k)² = a²

Director Circle

Director circle is a circle that intersects the ellipse at its endpoints (vertices) and is tangent to the ellipse at its foci.

For an ellipse with semi-major axis a and semi-minor axis b, the director circle has its center at the origin and its radius r is given by:

r = a²/b

The director circle’s equation is:

x² + y² = (a²)/(b²)​(x² + y²)

Examples of Ellipse

Some of the examples of ellipse are:

• Planetary Orbits: The orbits of planets around the sun and moons around planets are elliptical.
• Egg Shape: The shape of a hen’s egg closely resembles an ellipse.
• Satellite Orbits: Elliptical orbits are often used by satellites around Earth.
• Architecture: Some architectural designs, like the elliptical arches in buildings, bridges, and cathedrals, are based on ellipses.
• Sports: Tracks in sports like running, cycling, and horse racing are often elliptical in shape.

Types of Ellipses

Ellipses can be classified based on their orientation, size, and position. Here are some types of ellipses:

• Horizontal Ellipse
• Vertical Ellipse

Horizontal Ellipse

An ellipse where the major axis is horizontal. Its equation is

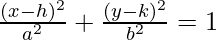
Where, (h, k) is the center of ellipse.

Vertical Ellipse

An ellipse where the major axis is vertical. Its equation is

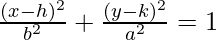
Where, (h, k) is the center of ellipse.

Note: Circle is the special case of ellipse where major and minor axis are same.

Formula for Ellipse

Some of the common formulas related to ellipse are:

• Area of Ellipse
• Perimeter of Ellipse
• Latus Rectum of Ellipse

Area of Ellipse

As we know the area of the circle is calculated using its radius, whereas the area of the ellipse depends on the length of the minor axis and major axis.

• Area of circle = πr²
• Area of ellipse = π × Semi-Major Axis × Semi-Minor Axis

Area of ellipse = πab

Where,

• a is the minor axis, and
• b is the major axis

Perimeter of Ellipse

Perimeter of an ellipse is the total length of the curve boundary. An ellipse has two axes, the major axis and the minor axis, both axis cross through the centre and intersects each other. The approximate formula to find the perimeter of an ellipse is:

P = 2π√{( a² + b²) / 2}

Where,

• a is the minor axis, and
• b is the major axis.

Latus Rectum Formula

Latus Rectum is defined as the line segments perpendicular to the major axis of the ellipse and passing through any of the foci in such a manner that their endpoints always lie on the ellipse.

The length of the Latus Rectum is defined in the diagram given below.

 

Length of the latus rectum for the ellipse is,

L = 2b²/a

Where,

• a is the minor axis, and
• b is the major axis.

Some Other Formulas and Equations

Some other equation related to ellipse include:

• Equatio of Tangent
• Equation of Normal

Equation of Tangent to Ellipse

There are various forms of equation of tangents to an ellipse:

Slope Form: If a line y = mx + c touchs the ellipse x² / a² + y² / b² = 1, then equation of tangent is given by:

• y = mx ± √[a²m² + b²]

Point Form: Equation of Tangent to an ellipse x² / a² + y² / b² = 1, at a point (x₁, y₁) is:

• xx₁ / a² + yy₁ / b² = 1

Paramatric Form: The parametric equations of the tangent line passing through the point (a cos ϕ, b sin ϕ) on the ellipse are:

• x = a cosϕ + a λ sinϕ
• y = b sinϕ − b λ cosϕ

Where λ is a parameter representing the slope of the tangent line.

Implicit Form: The implicit equation of the tangent line to the ellipse at the point (a cos ϕ, b sin ϕ) is given by:

• (x sin ϕ – y cos ϕ)²/a² + (x sin ϕ + y cos ϕ)²/a² = 1

Equation of Normal to Ellipse

If a line y = mx + c touchs the ellipse x² / a² + y² / b² = 1, then equation of tangent is given by:

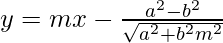
Summary

 In summary,

Aspect	Formula/Equation
General Equation
Parametric Equation	x = a cos (θ), y = b sin (θ)
Eccentricity
Foci	(±ae, 0)
Center	(h, k)
Major Axis Length	2a
Minor Axis Length	2b
Focus-Directrix Relation	PF1​ + PF2 ​= 2a
Latus Rectum Length	2b2/a
Area	A = πab
Perimeter	P ≈ 4aE(e), where E(e) is the complete elliptic integral of the second kind.
Slope of Tangent Line
Horizontal Directrix	y = – b2/a
Vertical Directrix	x = – a2/b

Also, Read

• Parabola
• Circle
• Hyperbola

Solved Examples on Ellipse

Example 1: If the length of the semi-major axis is given as 10 cm and the semi-minor axis is 7 cm of an ellipse. Find its area.

Solution: 

Given, the length of the semi-major axis of an ellipse, a = 10 cm

Length of the semi-minor axis of an ellipse, b = 7 cm

We know the area of an ellipse using the formula;

Area = π x a x b

Area = π x 10 x 7

Area = 70 x π

Therefore Area = 219.91 cm²

Example 2: For an ellipse, the length of the semi-major axis is 8 cm and the semi-minor axis is 3 cm then find its area.

Solution: 

Given:

Length of semi-major axis of the ellipse (a) = 8 cm

Length of semi-major axis of the ellipse (b) = 3 cm

Formula for the area of the ellipse:

Area = π x a x b

Area = π x 8 x 3

Area = 24 π cm²

Example 3: Find the lengths for the major axis and minor axis of equation 7x²+3y²= 21

Solution: 

Given equation is  7x²+3y²= 21

Dividing both sides by 21, we get

x²/3 + y²/7 = 1

We know that, Standard Equation of Ellipse

x²/b²+y²/a² = 1 

As the foci lies on y-axis, for the above equation , the ellipse is centered at origin and major axis on y-axis then;

b² = 3
b = 1.73

a² = 7
a = 2.64

Thus,

Length of Major Axis = 2a 
                                 = 5.28

Length of Minor Axis = 2b 
                                 =  3.46 

FAQs on Ellipse

What is an ellipse?

When a plane, intersects a cone at an angle with respect to the base the curve formed is called an ellipse. It is the locus of points, whose sum of the distances from two foci is always constant.

What is the major and minor axis of an ellipse?

Ellipses are distinguished by two axes running along the x and y axes:

• Major Axis: The major axis is the ellipse’s longest diameter, running through the center from one end to the other at the broadest part of the ellipse. 
• Minor Axis: The minor axis is the shortest diameter of an ellipse that crosses through the center at its narrowest point. Half of the major axis is the semi-major axis, and half of the minor axis is the semi-minor axis.

What is the Area of an ellipse?

The area of the ellipse is the region covered by the shape in the two-dimensional plane. It is given by:

Area = πab

where 
a is the semi-major axis
b is the semi-minor axis

What is the equation of an ellipse?

Equation of the ellipse is given by:

(x²/a²)+(y²/b²) = 1

What are the Asymptotes of Ellipse?

Asymptotes are lines drawn parallel to the curve and it is assumed that they meet the curve at infinity. Ellipse has no asymptote.

A

anjalishukla1859

Follow

Improve