Absolute Value of a Complex Number

The absolute value, or modulus, of a complex number measures its distance from the origin on the complex plane. If you have a complex number z = a + ib, where a is the real part while ib is the imaginary part of the complex number in which i is known as iota and b is a real number. Then the absolute value of x is denoted as |z|.

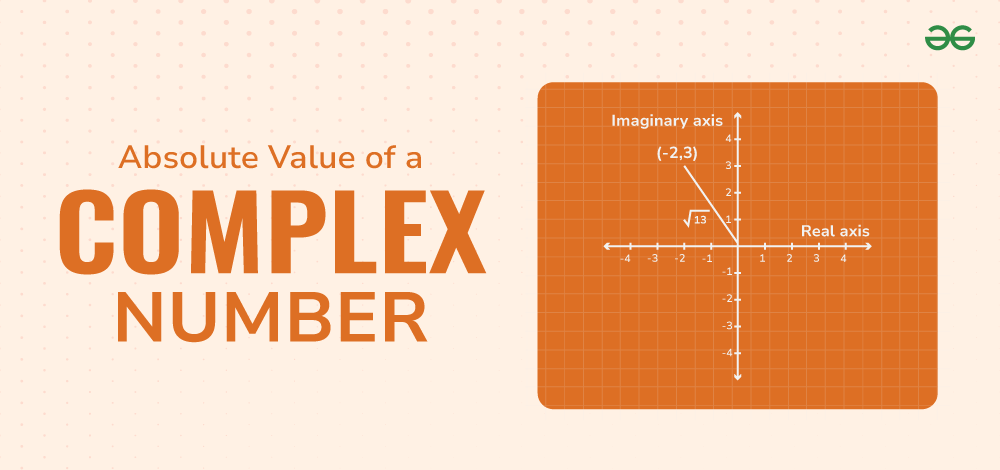
Absolute Value of a Complex Number

• Real Number: A real number is a number that is present in the number system which can be positive, negative, integer, rational irrational, etc. For example, 23, -3, 3/6.
• Imaginary Number: Imaginary numbers are those numbers that are not real numbers. For example, √3, √11, etc.
• Zero Complex Number: A zero complex number is a number that has its real and imaginary parts both equal to zero. For example, 0+0i.

Absolute Value of Complex Number

The absolute value(Modulus) of a number is the distance of the number from zero. Absolute value is always represented in the modulus(|z|) and its value is always positive. So, the absolute value of the complex number Z = a + ib is 

|z| = √ (a² + b²)

So, the absolute value of the complex number is the positive square root of the sum of the square of real part and the square of the imaginary part, i.e., 

Proof of Absolute Value of Complex Numbers

Let us consider the mode of the complex number z is extended from 0 to z and the mod of a, b real numbers is extended from a to 0 and b to 0. So these values create a right angle triangle in which 0 is the vertex of the acute angle

So, using Pythagoras theorem, we get, 

|z|² = |a|² + |b|²

⇒ |z| = √(a² + b²)

Now, in the sets of complex numbers z₁ > z₂ or z₁ < z₂ has no meaning but |z₁| > |z₂| or |z₁| < |z₂| has meaning because |z₁| and |z₂| is a real number. 

Properties of Modulus of a Complex Number

Some of the common properties of modulus of complex number are:

1. |z| = 0 ⇔ z = 0i, i.e., Re(z) = 0 and Im(z) = 0
2. |z| = |[Tex]\bar{z}    [/Tex]| = |-z|
3. -|z| ≤ Re(z) ≤ |z|, -|z| ≤ Im(z) ≤ |z|
4. z.[Tex]\bar{z}    [/Tex] = |z²|
5. |z₁z₂| = |z₁||z₂|
6. |z₁ / z₂| = |z₁|/|z₂|
7. |z₁ + z₂|² = |z₁| + |z₂| + 2Re(z₁[Tex]\bar{z}_2    [/Tex])
8. |z₁ – z₂|² = |z₁| + |z₂| – 2Re(z₁[Tex]\bar{z}_2    [/Tex])
9. |z₁ + z₂|² ≤ |z₁| + |z₂|
10. |z₁ – z₂|² ≥ |z₁| – |z₂|
11. |az₁ – bz₂|² + |bz₁ + az₂|² = (a² + b²)(|z₁|² + |z₂|²) Or |z₁ – z₂|² + |z₁ + z₂|² = 2(|z₁|² + |z₂|²)
12. |zⁿ| = |z|ⁿ
13. 1/z = a – ib/a² + b² =[Tex] \bar{z}   [/Tex]/|z|²

Example: Calculate absolute value of

• z = 3 + 4i
• z = 5 + 6i

Solution:

(i) z = 3 + 4i

Thus, |z| = √(3² + 4²)

⇒ |z| = √(9 + 16)

⇒ |z| = √25

⇒ |z| = ±5

(ii) z = 5 + 6i

|z| = √(5² + 6²)

⇒ |z| = √(25 + 36)

⇒ |z| = √61

Argument of Complex numbers

The argument of the complex number is the angle inclined from the real axis in the direction of the complex number that represents on the complex plane or argand plan. 

θ = tan^-1(b/a)

OR

arg(Z) = tan^-1(b/a)

Here, Z = a + ib

Properties of Argument of Complex Number

Some of the common properties of argument of complex numbers are:

• arg(Zⁿ) = n arg(Z)
• arg (Z₁/ Z₂) = arg (Z₁) – arg (Z₂)
• arg (Z₁ Z₂) = arg (Z₁) + arg (Z₂)

Example: Find the argument for

• z = 2 + 2i
• z = -4 + 4i

Solution:

(i) z = 2 + 2i

θ = tan^-1(2/2)

⇒ θ = tan^-1(1)

⇒ θ= 45°

(ii) z = -4 + 4i

θ = tan^-1(4/-4)

⇒ θ= tan^-1(-1)

⇒ θ = -45°

It is important to note here that  the angle θ =-45° is in 4^th quadrant, 

while we always measure angle with the positive x-axis. 

So, we will have to add 180° to the answer to obtain the real  opposite angle.

So, θ = 180° + (-45°)

⇒ θ = 135°

So , the above complex number will make an angle of 135° with the positive x-axis.

Related Articles:

• What is Z Bar in Complex Numbers?
• Polar and Exponential Forms of Complex Numbers
• Is Every Real Number a Complex Number?

Sample Problems on Absolute Value of a Complex Number

Q1: Find the absolute value of z = 4 + 8i

Solution:

Given complex number is z = 4 + 8i

As we know that the formula of absolute value is

|z| = √ (a² + b²)

So, a = 4, and b = 8, we get

|z| = √(4² + 8²)

|z| = √80

Q2: Find the absolute value of z = 2 + 4i

Solution:

Given complex number is z = 2 + 4i

As we know that the formula of absolute value is

|z| = √ (a² + b²)

So, a = 2, and b = 4, we get

|z| = √(2² + 4²)

|z| = √20

Q3: Find the angle of the complex number: z = √3 + i

Solution:

Given complex number is z = √3 + i

As we know, that 

θ = tan^-1(b/a)

So, a = √3 , and b = 1, we get

θ = tan^-1(1/ √3 )

θ = 30°

Q4: Find the angle of the complex number: z = 6 + 6i

Solution:

Given complex number is z = 6 + 6i

As we know, that 

θ = tan^-1(b/a)

So, a = 6 , and b = 6, we get

θ = tan^-1(6/6)

θ = 45°

Q5: Convert z =  5 + 5i into polar form

Solution:

Given complex number is z = 5 + 5i

As we know that 

Z = r(cos θ + isin θ) …(1)

Now, we find the value of r

r = √(5² + 5²)

r = √(25 + 25)

r = √50

Now we find the value of θ

θ = tan^-1(5/5)

θ = tan^-1(1)

θ = 45°

Now put all these values in eq(1), we get

Z = √50(cos 45° + isin 45°)

Q6: Convert z =  2 + √3i into polar form

Solution:

Given complex number is z = 2 + 2√3i

As we know that 

Z = r(cos θ + isin θ) …(1)

Now, we find the value of r

r = √(2² + (2√3)²)

r = √(4 + 12)

r = √16

r = 4

Now we find the value of θ

θ = tan^-1(2√3/2)

θ = tan^-1(√3)

θ = 60°

Now put all these values in eq(1), we get

Z = 4(cos 60° + isin 60°)

FAQs on Absolute Value of a Complex Number

Define absolute value of complex number.

Absolute value (or modulus) of a complex number z = a + bi, where a and b are real numbers and i is the imaginary unit, is defined as the distance of z from the origin in the complex plane.

How do you find the absolute value of a complex number?

To find the absolute value of a complex number z = a + bi:

1. Find square the real and imaginary part: a² and b².
2. Add the squares: a² + b².
3. Take the square root of the sum: ∣z∣ = [Tex]\sqrt{a^2 + b^2}[/Tex].

What is the geometric interpretation of the absolute value of a complex number?

Geometrically, the absolute value of a complex number z = a + bi represents the distance from the point (a, b) to the origin (0, 0) in the complex plane.

Can the absolute value of a complex number be negative?

No, the absolute value of a complex number is always a non-negative real number.

What is the absolute value of a purely real number?

If z = a + 0i is a purely real number, then its absolute value is ∣z∣= √(a² + 0²) = ∣a∣, which is simply the absolute value of the real part.

What is the absolute value of a purely imaginary number?

If z = 0 + bi is a purely imaginary number, then its absolute value is ∣z∣= √(0² + b²) = ∣b∣, which is the absolute value of the imaginary part.

What is the absolute value of zero?

The absolute value of zero is ∣0∣ = 0.

N

neeraj kumar 13

Follow

Improve