Satz des Thales – Einführung, Beweis und Anwendung

Der Satz des Thales besagt, dass ein rechtwinkliges Dreieck entsteht, wenn wir über einer Strecke einen Halbkreis konstruieren und einen beliebigen Punkt auf diesem Halbkreis mit der Strecke als Durchmesser zu einem Dreieck verbinden.
Der Kreis aus der Definition heißt Thaleskreis. Der Durchmesser bildet dabei stets die Hypotenuse des Dreiecks. Das heißt, der rechte Winkel liegt bei dem Eckpunkt des Dreiecks, der auf dem Thaleskreis liegt.

Eine gängige Formulierung des Satzes des Thales lautet:

Ein Dreieck, bei dem ein Eckpunkt auf einem Halbkreis über der gegenüberliegenden Seite liegt, ist rechtwinklig.

Es gilt auch die Umkehrung des Satzes:

Bei jedem rechtwinkligen Dreieck liegt der Eckpunkt mit dem rechten Winkel auf einem Halbkreis über der Hypotenuse (Seite gegenüber dem rechten Winkel).

Wir können auch kurz sagen: Jedes rechtwinklige Dreieck hat einen Thaleskreis.

Der Satz des Thales hat eine lange Geschichte in der Mathematik. Er wurde bereits vor mehr als Jahren durch den griechischen Mathematiker und Philosophen Thales von Milet bewiesen, von dem auch der Name Thaleskreis stammt.

Auch wir wollen nun einen Beweis des Satzes betrachten. Dazu verbinden wir den Eckpunkt mit dem Mittelpunkt der Strecke und beschriften die Winkel.

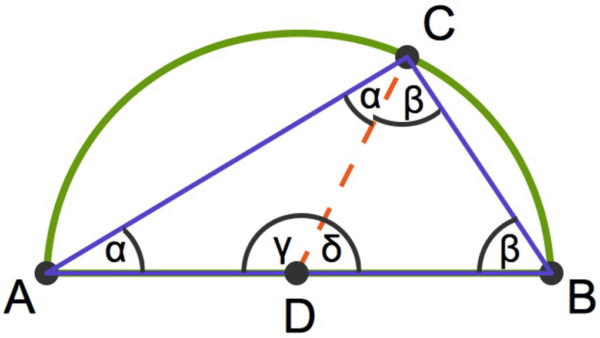
Da den Durchmesser des Thaleskreises bildet, ist auch Mittelpunkt des Kreises. Die Strecken , und haben also alle die Länge des Kreisradius . Wir erhalten somit zwei gleichschenklige Dreiecke: und .

In einem gleichschenkligen Dreieck sind die Basiswinkel stets gleich groß. Daher tauchen die Winkel und als Teile des Winkels bei auf. Nach dem Satz des Thales müsste hier die Formel gelten. Die Winkelsumme in einem Dreieck ist immer . Wir stellen die Gleichung für die Winkelsumme im Dreieck auf:

Die letzte Zeile der Gleichung besagt genau das, was wir zeigen wollten, und liefert damit den Beweis für den Thaleskreis.

Alternativer Beweis:

Einen geometrischen Beweis für den Satz des Thales liefert die folgende Konstruktion:

• Zeichne einen Kreis.
• Zeichne zwei Durchmesser 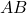und in den Kreis ein und markiere deren Endpunkte auf dem Kreis.
• Verbinde die Punkte , , und 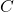zu einem Viereck.

Das so konstruierte Viereck ist stets ein Rechteck, da beide Diagonalen Kreisdurchmesser sind. Das heißt, sie sind gleich lang und halbieren sich gegenseitig. Das Dreieck ist somit bei rechtwinklig und ein beliebiger Punkt auf dem Kreis mit Durchmesser .

Hinweis: Der Beweis für den Satz des Thales kann auch durch das Skalarprodukt von Vektoren erfolgen. Dazu wird allgemein gezeigt, dass gilt: . Damit stehen die Vektoren und senkrecht. Das heißt, es gibt einen rechten Winkel bei .

Wir wollen nun einige Beispiele von Anwendungsaufgaben für den Satz des Thales betrachten.

Mit dem Thaleskreis kann ein rechtwinkliges Dreieck mit zwei vorgegebenen Seitenlängen konstruiert werden.

Dazu wird zunächst die Seite gegenüber dem rechten Winkel gezeichnet und darüber mit dem Zirkel der Thaleskreis gezogen. Der dritte Eckpunkt ist der Schnittpunkt des Thaleskreises mit einem Kreis um einen Eckpunkt mit der gegebenen Seitenlänge. Im oberen Beispiel ziehen wir einen Kreis um mit Radius und erhalten als Schnittpunkt dieses Kreises mit dem Thaleskreis.

Auch die Konstruktion von Kreistangenten ist mit dem Satz des Thales möglich.

Eine weitere Anwendung des Satzes des Thales bzw. seiner Umkehrung ist die Berechnung von Winkeln. Wir können anhand des Satzes des Thales rechte Winkel finden und darüber fehlende Winkel in einer Figur berechnen.

Aussage: Jedes Dreieck, das einen Thaleskreis hat, ist rechtwinklig. Dabei ist der Durchmesser des Kreises stets die Hypotenuse des Dreiecks. 

Umkehrung: Jedes rechtwinklige Dreieck besitzt einen Thaleskreis. Dieser hat die Hypotenuse des Dreiecks als Durchmesser.  

Anwendung: 

• Konstruktion von rechten Winkeln und Kreistangenten
• Nachweis von rechten Winkeln und Winkelberechnung