Partielle Integration – Formel, Herleitung und Beispiele

Erfahre, wie partielle Integration eine Regel zur Berechnung von Integralen darstellt, ähnlich der Umkehrung der Produktregel beim Ableiten. Entdecke die Formel und Beispiele für unbestimmte und bestimmte Integrale.

Inhaltsverzeichnis zum Thema Partielle Integration

Partielle Integration im Überblick

  • Partielle Integration ist eine Regel zur Berechnung von Integralen.

  • Die partielle Integration entspricht einer Umkehrung der Produktregel beim Ableiten.

  • Partielle Integration funktioniert nur bei der Integration von Funktionen f der Form f(x) = u^\prime(x) \cdot v(x). Unter dem Integral steht ein Produkt von Funktionen, dabei ist einer der Faktoren eine abgeleitete Funktion.
  • Als partielle Integration bezeichnet man die Formel:
    \displaystyle \int u^\prime(x) \cdot v(x)~\text{d}x = u(x) \cdot v(x) - \displaystyle\int u(x) \cdot v^\prime(x) ~\text{d}x
Partielle Integration: Lernvideo

Quelle sofatutor.com

Partielle Integration einfach erklärt

Die partielle Integration ist eine Regel zur Berechnung von Stammfunktionen oder bestimmten Integralen. Um die Regel verwenden zu können, muss der Integrand f, also die Funktion unter dem Integral, die Form f= u^\prime \cdot v haben.
Die Integration heißt partiell, weil jeweils nur einer der beiden Faktoren integriert wird.

Formel für partielle Integration

Die Voraussetzung zur Verwendung der partiellen Integration ist, dass sich die zu integrierende Funktion f als Produkt der Form f = u^\prime \cdot v schreiben lässt. Die Funktionen u^\prime und v sind Hilfsfunktionen, die nur dazu dienen, die Regel der partiellen Integration anzuwenden. Die partielle Integration für unbestimmte Integrale, also Stammfunktionen, ist die folgende Formel:

\displaystyle \int f(x) ~\text{d}x = \int u^\prime(x) \cdot v(x) ~\text{d}x = u(x) \cdot v(x) - \int u(x) \cdot v^\prime(x) ~\text{d}x

Der Term u(x) \cdot v(x) ist bereits ein Teil der Stammfunktion von u^\prime(x) \cdot v(x) und muss gar nicht mehr integriert werden. Das Integral auf der rechten Seite der Gleichung muss berechnet werden. Wenn dieses Integral leichter zu berechnen ist als das auf der linken Seite der Gleichung, kann das Integral durch partielle Integration bestimmt werden.

Ganz analog kann man partielle Integration auch zur Berechnung bestimmter Integrale verwenden. Die Formel sieht dann so aus:

\displaystyle \int_a^b f(x) ~\text{d}x =\int u^\prime(x) \cdot v(x) ~\text{d}x = \Bigl[u(x) \cdot v(x) \Bigr]^b_a -\int^b_a u(x) \cdot v^\prime(x) ~\text{d}x

Beispiel für partielle Integration

Um die Verwendung der partiellen Integration kennenzulernen, berechnen wir das Integral der Funktion f(x) = e^x \cdot x.
Wir können f als Produkt einer abgeleiteten Funktion u^\prime(x) und einer Funktion v(x) schreiben, indem wir u^\prime(x) = e^x und v(x) = x setzen. Bei der partiellen Integration bestimmen wir zuerst eine Stammfunktion u(x) von u^\prime(x). In unserem Beispiel ist u(x) = e^x, denn die Funktion u(x) = e^x hat die Ableitung u^\prime(x) = e^x. Als Nächstes berechnen wir die Ableitung von v(x)=x. Die Ableitung ist v^\prime(x) = 1.

Jetzt können wir diese Funktionen in die Formel einsetzen:

\begin{array}{rcl} \displaystyle \int \underbrace{e^x}_{u^\prime(x)} \cdot \underbrace{x}_{v(x)} ~\text{d}x &=& \underbrace{e^x}_{u(x)} \cdot \underbrace{x}_{v(x)} - \displaystyle \int \underbrace{e^x}_{u(x)} \cdot \underbrace{1}_{v^\prime(x)} ~\text{d}x \\ &=& e^x \cdot x - \displaystyle \int e^x ~\text{d}x \\ &=& e^x \cdot x - e^x \end{array*}

Das Integral \displaystyle \int e^x ~\text{d}x am Ende der partiellen Integration ist viel leichter zu berechnen als das Integral \displaystyle \int e^x \cdot x ~\text{d}x am Anfang. Wir konnten es hier elementar berechnen, denn die Stammfunktion von u(x) \cdot v^\prime(x) = e^x ist wieder e^x.
An diesem Beispiel siehst du, wie durch partielle Integration ein schwieriges Integral auf ein einfacheres reduziert wird.

Um zu überprüfen, dass F(x)=e^x \cdot x - e^x eine Stammfunktion von f(x)=e^x \cdot x ist, berechnen wir zur Probe die Ableitung von F(x):

F^\prime(x)=(e^x \cdot x - e^x)^\prime = (e^x \cdot x + e^x \cdot 1) - e^x = e^x \cdot x =f(x)

Auf die gleiche Weise wie oben können wir auch das bestimmte Integral in den Grenzen a = 0 und b = 1 berechnen:

\begin{array}{rcl} \displaystyle \int_0^1 e^x \cdot x ~\text{d}x &=& [e^x \cdot x]^1_0 - \displaystyle \int_0^1 e^x \cdot 1 ~\text{d}x \\ &=& [e^x \cdot x]^1_0 - [e^x]^1_0 \\ &=& (e^1 \cdot 1 - e^0 \cdot 0) - (e^1-e^0) \\ &=& e^1-e^1 =0 \end{array}

Partielle Integration – Herleitung der Formel

Wir haben oben die Produktregel der Ableitung benutzt, um zu überprüfen, ob die berechnete Stammfunktion korrekt ist. Auf ähnliche Weise können wir auch zeigen, dass die Formel der partiellen Integration stimmt.

In der Formel

\displaystyle \int u^\prime(x) \cdot v(x) ~\text{d}x = u(x) \cdot v(x) - \int u(x) \cdot v^\prime(x) ~\text{d}x

bringen wir das Integral von der linken auf die rechte Seite und erhalten:

\displaystyle \int u^\prime(x) \cdot v(x) ~\text{d}x + \int u(x) \cdot v^\prime(x) ~\text{d}x = u(x) \cdot v(x)

Nach der Summenregel für Integrale lassen sich die beiden unbestimmten Integrale auf der linken Seite zu einem Integral zusammenfassen:

\displaystyle \int \left[u^\prime(x) \cdot v(x) + u(x) \cdot v^\prime(x) \right] ~\text{d}x = u(x) \cdot v(x)

Auf der rechten Seite steht das Produkt der Funktionen u und v. Berechnen wir mit der Produktregel der Differentiation die Ableitung von u(x) \cdot v(x), erhalten wir:

\big[u(x) \cdot v(x)\big]^\prime = u^\prime(x) \cdot v(x) + u(x) \cdot v^\prime(x)
Dies ist genau der Integrand der linken Seite. Die Funktion u(x) \cdot v(x) ist also eine Stammfunktion des Integranden u^\prime(x) \cdot v(x) + u(x) \cdot v^\prime(x).

Anwendungen partieller Integrationen

Um die Methode der partiellen Integration sinnvoll anzuwenden, kommt es darauf an, die Hilfsfunktionen u und v geschickt zu wählen. Für diese Wahl gibt es keine allgemeinen Regeln. Als Orientierung für viele Anwendungen gilt:

  • Die Funktion 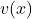v(x) sollte beim Ableiten einfacher werden.
  • Von der Funktion u^\prime(x) sollten wir die Stammfunktion u(x) bereits kennen.
  • Partielle Integration funktioniert immer dann, wenn der Integrand das Produkt einer rationalen Funktion und einer Exponentialfunktion ist.
  • Die e-Funktion setzen wir bei der partiellen Integration gleich u^\prime(x), denn deren Stammfunktion ist wieder eine e-Funktion.
  • Die rationale Funktion setzen wir gleich 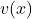v(x), denn beim Ableiten erhält man eine rationale Funktion kleineren Grads.
  • Durch wiederholte partielle Integration kann man die Berechnung der Stammfunktion letztlich auf die Exponentialfunktion zurückführen.

Wir zeigen noch ein anderes Beispiel partieller Integration, um die Methode besser kennenzulernen: Wir suchen die Stammfunktion des natürlichen Logarithmus \ln(x). Durch Ableiten wird die Funktion einfacher, denn (\ln(x))^\prime = \frac{1}{x}. Also setzen wir v(x) = \ln(x). Es fehlt noch der Faktor u^\prime(x). Da wir nur die Stammfunktion von \ln(x) berechnen wollen, setzen wir u^\prime(x) = 1. Eine Stammfunktion von u^\prime(x) = 1 ist dann u(x) = x. Nun können wir partiell integrieren:

\begin{array}{rcl} \displaystyle \int 1 \cdot \ln(x) ~\text{d}x &=& x \cdot \ln(x) - \displaystyle \int x \cdot \frac{1}{x}~\text{d}x \\ &=& x \cdot \ln(x) - \displaystyle \int \frac{\not{\!x}}{\not{\!x}}~\text{d}x \\ &=& x \cdot \ln(x) - \displaystyle \int 1 ~\text{d}x \\ &=& x \cdot \ln(x) - x \end{array}

Häufig gestellte Fragen zum Thema Partielle Integration

Partielle Integration ist eine Regel zur Integration von Funktionen f, die sich als Produkt der Form f = u^\prime \cdot v schreiben lassen.

Du schreibst den Integranden f als Produkt der Form f = u^\prime \cdot v. Dann bestimmst du die Stammfunktion u von u^\prime und die Ableitung v^\prime von v. Diese setzt du in die Formel der partiellen Integration ein und berechnest das Integral \int u(x) \cdot v^\prime(x) ~\text{d}x.

u und v sind Hilfsfunktionen, anhand derer du eine Funktion der Form f = u^\prime \cdot v durch partielle Integration integrieren kannst.

Ist der Integrand f das Produkt aus der Ableitung u^\prime und einer weiteren Funktion v, kannst du das Integral mit partieller Integration bestimmen. Partielle Integration kannst du beispielsweise anwenden, wenn der Integrand eine trigonometrische Funktion wie \cos^2 oder \sin^2 oder eine e-Funktion als Faktor enthält.

Die Funktionen \sin^2 oder \cos^2 kann man nicht direkt integrieren. Hier helfen Integrationsregeln, z. B. eine doppelte partielle Integration. Man erhält dabei zwar wieder das ursprünglich zu berechnende Integral, aber die Gleichung lässt sich so auflösen, dass man dieses Integral berechnen kann.
Ist der Integrand ein Produkt aus einer e-Funktion und einer Potenzfunktion, kann man mehrmals partiell integrieren. Dabei werden so lange Ableitungen von Potenzfunktionen und Stammfunktionen von Exponentialfunktionen berechnet, bis die Ableitung der Potenzfunktion eine Konstante ergibt.

Für beide Integrationsregeln muss der Integrand ein Produkt von Funktionen sein. Aber die Gestalt des Produkts ist bei Substitution und partieller Integration verschieden:

  • Bei der Substitution ist der Integrand das Produkt der Ableitung einer äußeren Funktionen und der inneren Ableitung.
  • Bei der partiellen Integration ist der Integrand das Produkt einer Funktion mit der Ableitung einer anderen Funktion.
  • Bei einer Substitution kommen also ineinander verschachtelte Funktionen vor, bei der partiellen Integration nicht.
  • Partielle Integration beruht auf der Umkehrung der Produktregel der Differentiation.
  • Substitution beruht dagegen auf der Umkehrung der Kettenregel.

Manche Funktionen lassen sich nicht direkt integrieren. Partielle Integration ist eine Methode, die Berechnung auf bereits bekannte Integrale zurückzuführen oder die Integration zu vereinfachen.

Mittels partieller Integration lässt sich in geeigneten Fällen die Berechnung von Stammfunktionen vereinfachen. Durch geschickte partielle Integration kann man die Berechnung unbekannter Integrale auf bereits bekannte Stammfunktionen zurückführen.

Das Produkt zweier Funktionen kann man nicht direkt integrieren. Nur wenn einer der beiden Faktoren die Ableitung einer bekannten Funktion ist, kann man die Regel der partiellen Integration verwenden.

Der Wert eines bestimmten Integrals kann negativ sein. Das geschieht z. B. dann, wenn der Integrand negative Werte annimmt. Aber auch die Vertauschung der Integralgrenzen kehrt das Vorzeichen eines bestimmten Integrals um und macht ein positives Integral zu einem negativen. Benutzt man Integration zur Berechnung von Flächeninhalten, ist zu beachten: Ein Flächeninhalt kann nicht negativ sein.

Super! Das Thema: kannst du schon! Teile deine Learnings und Fragen mit der Community!

Alle Artikel aus dem Fach Mathematik